教師なし学習におけるクラスタ数の決定方法について
今回の内容
今回は、教師なし学習におけるクラスタ数の決定方法について書いていこうと思います。以前、授業でKMeans法でのクラスタリングを学びました。そこで復習のためにPythonで実装してみようと思い、今回取り組んでいます。その中で、クラスタ数の決定方法は学んでいなかったことから少しまとめました。
用いたデータ
scikit-learnのワインの種類に関するデータを用いました。178個のデータに関してアルコールやマグネシウム量など全部で13個の特徴量が記載さています。
前処理や次元削減に関しては今回の内容と離れるため書いていません。前処理にはMinMaxScalerを利用し、次元削減では主成分分析を用いて13次元から2次元にしてから以下の操作を行いました。
①SSEを利用する
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
SSE = []
for i in range(1,11):
kmeans = KMeans(n_clusters=i, random_state=0)
kmeans.fit(two_dimension)
SSE.append(kmeans.inertia_)
plt.plot(range(1,11),SSE,marker='o')
plt.xlabel('cluster_number')
plt.ylabel('SSE')
plt.show()
<出力画像>
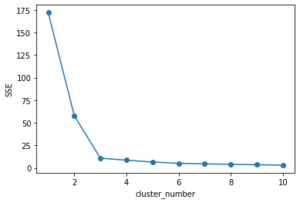
<解説>
SSEとは、各点とクラスタの中心の距離の和を計算したものです。もちろん、数が小さい方がよいです。グラフを見ると、cluster_numberが3より大きい数の時、値がほとんど変化していません。よって、クラスタの数は3が適していると推測します。
しかし、これでは単純すぎる可能性があります。よってシルエットスコアも考えることでクラスタ数が3で適切であるか判断したいと思います。
②シルエットスコアを利用する
from sklearn.metrics import silhouette_score
SILHOUETTE = []
for i in range(2,8):
kmeans = KMeans(n_clusters=i, random_state=0)
kmeans.fit(two_dimension)
y_pred = kmeans.fit_predict(two_dimension)
score = silhouette_score(two_dimension, y_pred)
SILHOUETTE.append(score)
plt.plot(range(2,8),SILHOUETTE,marker='o')
plt.xlabel('cluster_number')
plt.ylabel('silhouette_score')
plt.show()
<出力画像>
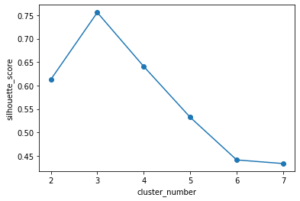
<解説>
以上が、シルエットスコアによって考えた結果です。(シルエットスコアの説明は長くなるため省略)これは、1に近いほど良いと考えるため、今回の結果ではクラスタ数が3である方がよいと判断することができます。
①と②の結果では、どちらもクラスタ数を3にする方がよいとわかりました。よって、クラスタ数を決定することができました。
クラスタ数決定後
クラスタ数を決定したら、KMeans法で実際にクラスタリングを行います。
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3)
y_pred = kmeans.fit_predict(two_dimension)
y_pred
#出力結果
array([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 0, 1, 1, 1, 1,
2, 1, 1, 1, 1, 2, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0])
出力結果より、0から2までの三つのクラスタに分けることができました。これを散布図にプロットすると以下の図になりました。
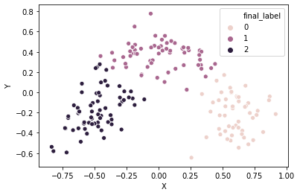
三つのクラスタに分かれています。
ただし、はっきりと集団に分けることはできませんでした…
参考
・【教師なし学習】機械学習でワインの品質判定を行ってみよう【scikit-learn】
https://obgynai.com/unsupervised-learning-machine-learning/
・Aurélien Géron(著)、scilit-learn、Keras、TensorFlowによる実践機械学習
・Andreas C. Muller(著)、Pythonではじめる機械学習


コメント入力