はじめに

今日予定していた記事が出来そうにないらしいので後日に回してなんか、適当に書こうと思ったのですが、先ほど「日本のコロナの謎」というものを見つけたので、世界的に使われているPCR検査に関してのある確率計算でもしてみようという話でもします。考察から読みたい方はこちらからどうぞ。

前提条件

まずは前提条件なのですが、色々見ていきたいので、文字で先に計算してあとで色々代入していきます。

ということで、ある人口に対して病気の割合を\alpha[%]、検査の精度を\beta[%]とします。また、ある人口をH人とします。

この時、

• 病気の人数:H\times\alpha [人]
• 病気でない人数:H\times(1-\alpha) [人]

となります。

病気の人

病気の人に検査をした場合、陽性の場合正解、陰性の場合不正解ということで、人数は次のようになります。

• 陽性の人数:H\times\alpha\times\beta [人]
• 陰性の人数:H\times\alpha\times(1-\beta) [人]

病気でない人

病気でない人に検査をした場合、陽性の場合不正解、陰性の場合正解ということで、人数は次のようになります。

• 陽性の人数:H\times(1-\alpha)\times(1-\beta) [人]
• 陰性の人数:H\times(1-\alpha)\times\beta [人]

陽性なのに病気でない確率

以上から陽性なのに病気でない確率を求めると

\displaystyle\frac{H\times(1-\alpha)\times(1-\beta)}{H\times\alpha\times\beta+H\times(1-\alpha)\times(1-\beta)} \displaystyle=\frac{\alpha\beta-\alpha-\beta+1}{2\alpha\beta-\alpha-\beta+1}

とこうなります。

陰性なのに病気である確率

同様に院生なのに病気である確率を求めると

\displaystyle\frac{H\times\alpha\times(1-\beta)}{H\times\alpha\times(1-\beta)+H\times(1-\alpha)\times\beta} \displaystyle=\frac{\alpha-\alpha\beta}{\alpha+\beta-2\alpha\beta}

となります。

グラフにしてみた

まずは感染者数データのソースですがこちら(札幌医科大学)です。こちらは100万人当たりの感染者数のグラフです。

3/24時点の情報で一番感染者数が多い国はイタリアということで、今回はイタリアの人全員に精度\beta%の検査を行ったと仮定します。このとき、この感染者数というものが100%正確な値であったとき、データより100万人中1057.31人なので、\alpha=0.00105731\times100\fallingdotseq0.1 [%]となります。

先ほどの式をグラフ化すると次のようになります。(Desmosにて作成

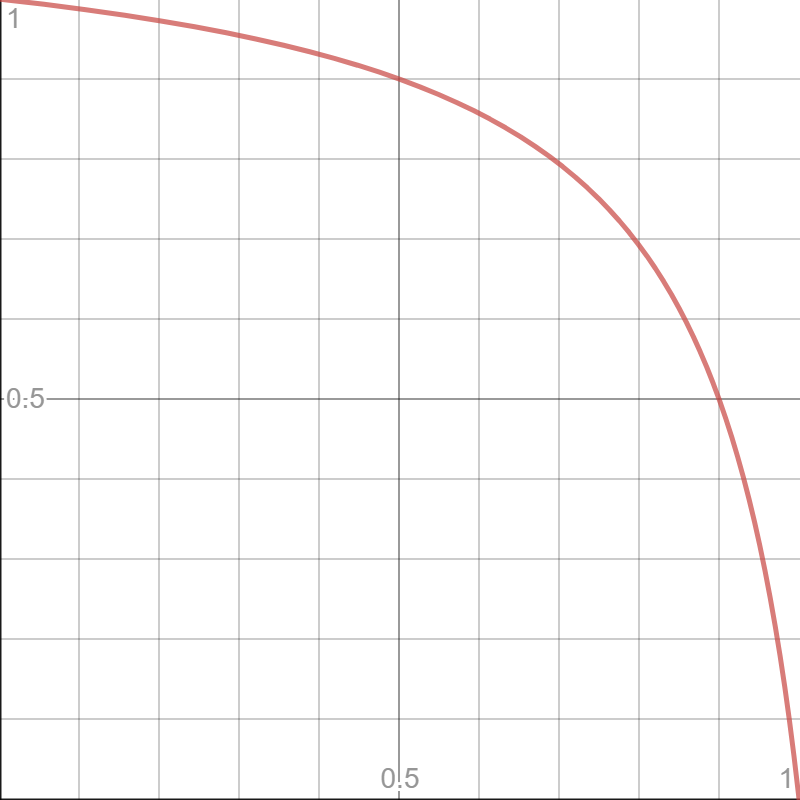
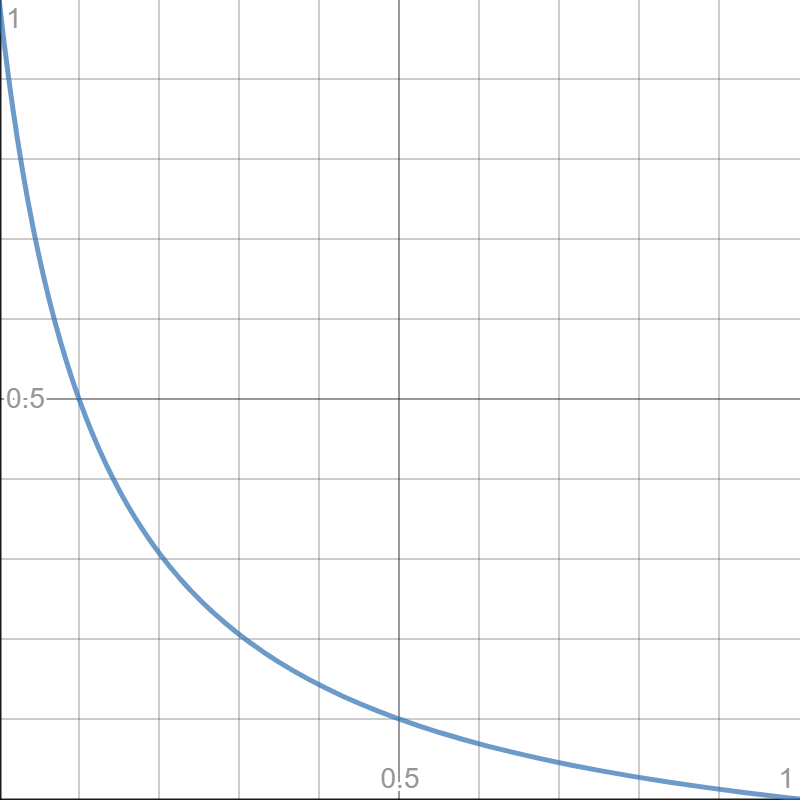
左:陽性なのに病気でない確率, 右:陰性なのに病気である確率

横軸は検査精度[%]で縦軸は上記確率です。見事に線対称になってて面白いなと思いました。

ここ(さいとう内科・循環器クリニック)によると世界中で多く行われている簡易検査であるPCR検査はおおむね精度が5割から7割程と言われているらしいのですが、このグラフを見た際、50%の精度の場合、陽性と出ても90%が陰性です。また、精度70%であっても約80%は陰性です。

逆に陰性であった場合、精度50%のとき10%が陽性、精度70%の場合4.5%が陽性です。

考察

この例で考えると今現在コロナに感染していないとされている人数のほうが感染しているとされている人数に比べて非常に割合が多いとされていますが、このPCR検査で陽性と診断されたという人数を鵜呑みにしていいのでしょうか。

このように検査精度が低い検査は陽性患者の数を増やすだけで悪影響しかなく、むだな軽症ですらない患者が増えてしまうような気がします。

感染者数が100%であるという前提でデータを扱ったり、イタリアの全員が検査を受けたという非現実的なデータの扱い方をしたので、隠れ患者がいる結果この人数になるとも考えられますが、この精度の高くないであろう検査の結果、重症になった患者が救われないということがあっては意味がないのではないでしょうか。

結論

PCR検査を多くの人に行っていない日本に対して批判しているような国があるとかないとかですが、日本の安易に精度の低い検査をいっぱいしないという選択は非常に論理的に、医療的には正しいことなのではないでしょうか。

未だに検査をしろと言っている方が周りにいた際にはこの話を教えてあげましょう。それに、コロナにかかっても大体死にません。ですが、下手に感染者を増やしてしまうとそれだけお医者さん一人が患者一人にさける時間が減ってしまい、すべての病気の致死率があがってしまう可能性さえあります。

イタリアのように医療崩壊してしまっている例もありますし、安易な外出は避け、うがい手洗いをしっかりしてインフルエンザ、ノロウイルス等を含めた病気に気を付けて新学期からがんばっていきましょう！

ということで、数学は嘘はつかないけど、嘘つきは数学を使うという話でした。情報の取捨選択というものはこういうのも含まれるから数学は大事なんだよっていうのを全世界の小中高校生に伝えたいですね。

追記

計算間違いなどありましたら教えてください。と思っていたのですが、既に根底を揺るがしてしまう問題を見つけてしまったり、細かいミスを沢山しているので、やっぱりいいです。

発見された間違い

せっかく見てもらったのにどこ間違ったかわかんないでもやもやさせたままなのもなんなので、間違えていた部分に関してここで説明していこうと思います。記事を読んでいた時点で引っかかってた人は情報強者かも!?

1. %の使い方がおかしい。

まずはこれなのですが、\alpha%, \beta%というのの使い方がおかしいですね。普通に小数として扱ってください。割合の扱い方が変でした。

2. 検査の精度が変

これに関してはほんとにこの話の根底を揺るがしてしまうのですが、検査の精度には「感度」と「特異度」という2種類のものがあり、ここで説明した精度はソース元によると「感度」のことです。(ちゃんと読んでないのがばれた。)ということで、友達が検索した結果、ソース元がなく申し訳ないのですが「特異度」に関しては100%らしいということでした。特異度が100%なのであれば、まずこの話が意味がないということになってしまうということで非常に残念なのですが、これは同時にモノの定義を正しく認識することの大事さを改めて認識させられるような話だなと感じました。

数学や、科学において、モノの定義というものは結果の違いを生んでしまったり、理解の違いを生んでしまうものであるということも説明できましたし、これを書いたことによって自分が新たな知識がえられたことをうれしく思うためにこのまま残そうとは思いますが、やはり、情報の取捨選択ってだいじなんやなってことですわ。言葉の定義、数字の扱い方、これらに騙されないようにやはり義務教育って重要なんだなって思った(小並感)。